# silver 4
문제
https://www.acmicpc.net/problem/2581
2581번: 소수
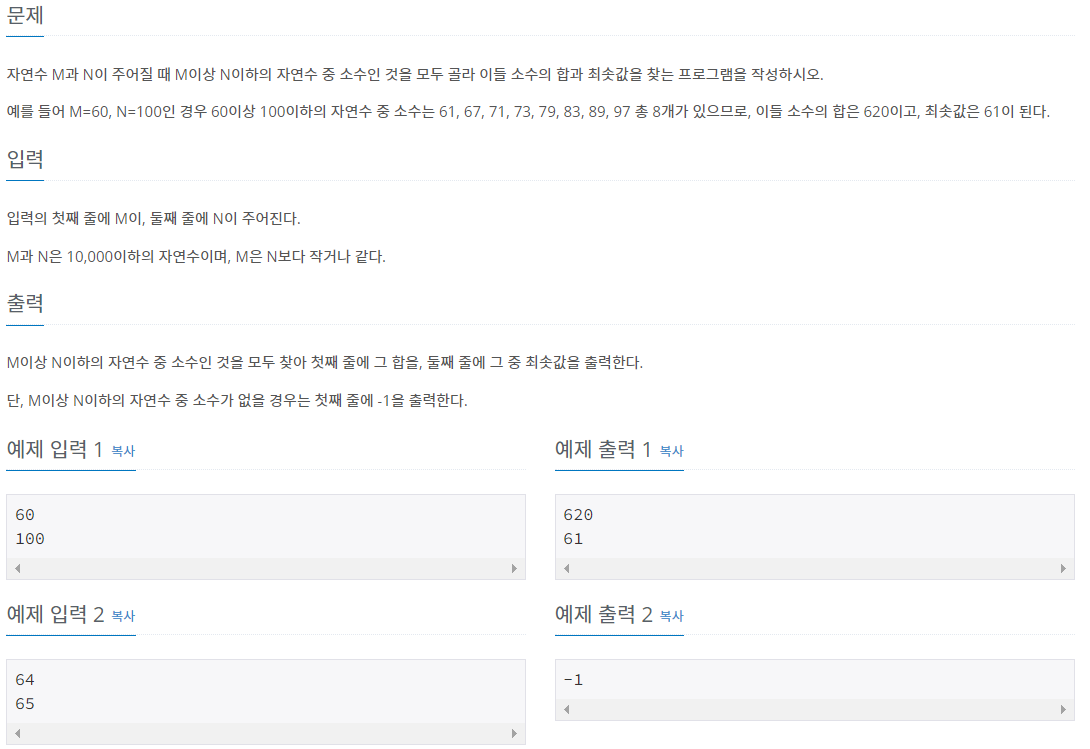
M이상 N이하의 자연수 중 소수인 것을 모두 찾아 첫째 줄에 그 합을, 둘째 줄에 그 중 최솟값을 출력한다. 단, M이상 N이하의 자연수 중 소수가 없을 경우는 첫째 줄에 -1을 출력한다.
www.acmicpc.net
코드
Ver 1)
#num이 소수인지 아닌지 판별하는 함수
def PrimeNum(num):
if num == 0 or num == 1: # 0, 1에 대해 예외처리를 해줘야 함!
return False
for k in range(2, num):
if num % k == 0: #2~n-1 로 나눴을 때 나눠짐 ==> 소수가 아님
return False
return True
#범위 input으로 받아오기
M = int(input())
N = int(input())
#comprehension으로 소수 리스트 완성
pnum = [i for i in range(M,N+1) if PrimeNum(i)] #if PrimeNum(i) == True
#소수가 존재하지 않을 경우를 위한 예외처리 - IndexError
try:
print("%d\n%d"%(sum(pnum), pnum[0]))
except IndexError:
print(-1)def Primenum의 시간복잡도 = O(N)
Ver 2)
import math #제곱근을 구하기 위해 math라이브러리 import
def PrimeNum(num):
if num == 0 or num == 1:
return False
for k in range(2, int(math.sqrt(num))+1): #루트 씌운후 정수형으로 변환 필요!!!
if num % k == 0:
return False
return True
M = int(input())
N = int(input())
pnum = [i for i in range(M,N+1) if PrimeNum(i)]
try:
print("%d\n%d"%(sum(pnum), pnum[0]))
except IndexError:
print(-1)def PrimeNum의 시간복잡도 = O(n^(1/2))
Ver 3)
import math
def PrimeNum(num):
arr = [True for i in range(num+1)]
arr[0],arr[1] = False, False
for i in range(2, int(math.sqrt(num))+1):
if arr[i] == True:
j=2
while i*j <= num:
arr[i*j]=False
j+=1
return arr
M = int(input())
N = int(input())
primeArray = PrimeNum(N)
pnum =[]
for i in range(M, N+1):
if primeArray[i] == True:
pnum.append(i)
else:continue
try:
print("%d\n%d"%(sum(pnum), pnum[0]))
except IndexError:
print(-1)def PrimeNum의 시간복잡도 = O(logn)
풀이
- Ver 1)
- 소수의 정의 이용
: 1 과 자신을 제외한 약수 존재 X
∴ for문을 통해 2 ~ n-1까지의 수로 나눔 → 나머지가 0이면 소수가 아님(False), 나누어 떨어지는 수가 없다면 소수(True)
- 소수일 경우 → pnum에 append
- sum()을 이용해 소수의 합, pnum[0]을 이용해 소수 中 최소값 구함
✓ try - except문을 통해 리스트가 비어있을 경우 (= 소수가 존재하지 않는 경우) 예외처리
- Ver 2)
- 약수의 성질을 이용
- 만약 2로 나눠진다면, n // 2와 동일한 수로는 나눠볼 필요가 없음. ⇒ 대칭적으로 삭제되어가는 방식
∴ 시간 복잡도를 줄이기 위해, 소수를 구하는 계산을 2 ~ √n 까지만 진행
- 제곱근 계산을 위해 math 라이브러리 import (sqrt 메소드 이용)
- 단, range의 범위로 들어가는 수는 int형이어야 하므로 제곱근 계산 후 int로 typecasting 필요
- Ver 3)
- 에라토스테네스의 체 적용
에라토스테네스의 체
1. 2부터 N까지의 모든 자연수를 나열한다.
2. 남은 수 중에서 아직 처리하지 않은 가장 작은 수 i를 찾는다.
3. 남은 수 중에서 i의 배수를 모두 제거한다.(i는 제거하지 않는다.)
4. 더 이상 반복할 수 없을 때까지 2번과 3번의 과정을 반복한다
... ❝ 예를 들어, 2의 배수인 4, 8, 16, ... 들은 당연히 약수로 2를 무조건 포함하고 있을 것이기에 자연스럽게 소수에서 탈락이다. 반면에 제일 앞에 등장한 2는 1과 자기 자신만을 약수로 가지므로 소수라고 할 수 있다. 따라서 맨 앞에 나온 숫자만 남겨놓고 그 뒤에 나오는 배수들을 전부 지워주다보면, 결과적으로 소수만 남게 됨을 알 수 있다. ❞
- i만 남겨놓고, i의 배수는 삭제하는 작업을 하기 위해 list 생성 : 인덱스 == 수, element == True / False
- True = 소수 , False = 소수가 아님을 의미
- 0과 1은 예외처리 하기 위해 False로 바꿔줌
- 범위를 줄이기 위해, 마찬가지로 제곱근에 해당하는 수 이하까지 진행함
- 각 arr의 element값이 True 인 경우 (== 소수인 경우) → 배수를 만들기 위해 j 가 등장하고 리스트 안에 배수를 전부 False로 바꿔준다
→ √n = n이 되기 위해 √n(자기자신)을 곱해야 함 -- 소수가 될 수 있는 마지노선 (가장 큰 수)
(∵앞에서부터 i의 배수는 다 삭제하므로 )
(그럼 나머지는?... → 걔넨 애초에 i의 배수에도 해당 안되므로 당연히 True로 남겨 두는게 맞다!)
다른 풀이
- 출처: https://www.acmicpc.net/source/11845966
def prime_list(n):
# 에라토스테네스의 체 초기화: n개 요소에 True 설정(소수로 간주)
sieve = [True] * n
# n의 최대 약수가 sqrt(n) 이하이므로 i=sqrt(n)까지 검사
m = int(n ** 0.5)
for i in range(2, m + 1):
if sieve[i] == True: # i가 소수인 경우
for j in range(i+i, n, i): # i이후 i의 배수들을 False 판정
sieve[j] = False
# n-1 까지의 소수 목록 산출
return [i for i in range(2, n) if sieve[i] == True]
A = int(input())
B = int(input())
L = prime_list(B+1)
idx = -1
for i in range(len(L)):
if L[i] >= A:
idx = i
break
if idx == -1:
print(idx)
else:
print(sum(L[i:]))
print(L[i])- sieve (=arr) 정의 시 for문 대신 [True] * n으로 정의함
- sqrt() 대신 **0.5 사용
- while문 대신 for문 사용: range ==> i*2 부터 시작, i*j대신 i씩 더해나가는 걸로 해결
- return을 아예 소수만 들어있는 리스트로 함
→ 범위 내 소수를 구할 때 리스트를 새로 생성할 필요가 없음 (if문으로 최솟값이 시작되는 인덱스 (idx)를 따로 저장
(근데 sum(L[idx:]))가 아닌가?... 어차피 break로 빠져나오고 i 값이 남아있는 상태여서 상관 없는듯 하다)
- 예외처리를 try-except 문이 아닌 idx == -1 인 경우로 해줬다.
'Algorithm > Beakjoon' 카테고리의 다른 글
| [Python] 백준 11718번_그대로 출력하기 (0) | 2022.08.01 |
|---|---|
| [Python] 백준 10951번_A+B - 4 (0) | 2022.07.30 |
| [Python] 백준 2460번_ 지능형 기차 2 (0) | 2022.07.26 |
| [Python] 백준 10818번_ 최소, 최대 (0) | 2022.07.26 |
| [Python] 백준 3460번_ 이진수 (0) | 2022.07.26 |
