반응형
1. 트라이가 뭐지?
단어를 순서대로 정렬하고 특정 인덱스에 있는 단어를 , 또는 특정 단어의 인덱스를 조회하고 싶은 경우 사용하는 자료구조이다. 주어지는 단어들을 정렬된채로 유지하는 데에 사용 가능한 자료구조는 트리셋, 우선순위큐도 가능할 것이다. 리스트에 넣어서 매번 정렬하기엔 시간 복잡도가 치명적이다. (이분 탐색을 사용해 자체적으로 순서를 유지하며 넣어주는 방법도 있지만 이건 제외하고)
이진검색 트리를 사용하면 logN이지만 문자열임을 감안했을 때 MlogN의 시간 복잡도가 소요된다는 것이다.
하지만 트리셋과 우선순위큐의 단점은 중간 그 어딘가에 존재하는 원소는 조회가 어렵다는 것이다. 그런 단점을 보완하고자 나온 구조가 바로 트라이(Trie) 구조이다.
즉, 트라이 알고리즘은 문자열을 정렬된 상태로 유지하되, 검색에 효율적인 알고리즘이다.
2. 트라이의 정의
- retrieval tree의 준말로, 영어 사전, 혹은 파일 계층 구조와 비슷한 애라고 생각하자
- 문자열을 (원하는 기준으로) 정렬하여 저장하고, 탐색도 빠르게 가능하다 (시간복잡도가 O(N))
- 기준을 유지한 채 새 문자열을 삽입하기도 쉽다 (겹치는 지점까지 타고 내려가서 남는거 뒤에 붙이면 되니까)
- 근데 이제 메모리를 엄청 잡아먹는...
트라이의 구조
이해를 돕기 위해, 트라이 구조의 대표 사용 예시인 영어 사전을 가정하여 설명하겠다.
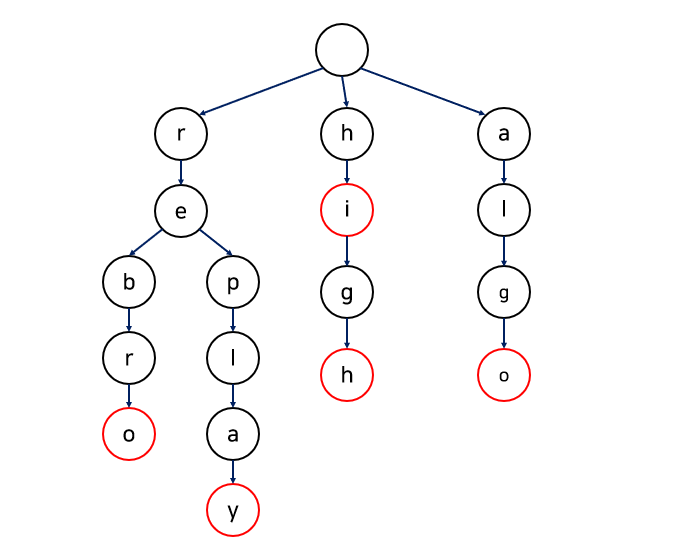
- 루트 노드는 항상 empty 상태이다. 여러가지 분기로 나뉘는 시작점을 하나로 묶어놓기 위해 필요한 역할.
- 그러므로 루트 노드의 자식 노드들은 'a' ~ 'z'처럼 각 단어의 첫 글자가 된다 (시작점)
- 타고 타고 내려가다,,, 그 끝에 마지막 노드(endOfNode)임을 표시해준다. 마지막 노드는 해당 문자열의 마지막 글자를 의미하겠다.
노드의 구성
class TrieNode {
// 자식으로 얼마나 올지 확실하지 않으면 map을 사용해 추가하자
HashMap<Character, TrieNode> child
boolean isEndOfNode //마지막 노드인지 검사
}- 공간 효율 측면에서도, 유동성 확보 측면에서도 Map을 사용하는게 나아보인다.
노드 추가
- root부터 시작해서, Map의 Character를 기준으로 한바퀴 돈다. (일치하는 것이 나올 때 까지)
- 있으면 그 하위로 타고 내려간다 (더 일치하는게 있을지도 모르니. 일치하는 것이 탐색동안 나오지 않을 때 까지 탐색 후 없으면 그 옆에 추가하고 isEndOfNode 표시를 해준다.
-> 이때, 하위로 들어가는 노드의 isEndOfNode는 그대로 둔다. (얘는 그냥 특정 문자열의 끝을 알려주기 위한 것이다) - 없으면 루트 노드의 자식노드로 추가해준다 (마지막 표시)
- 있으면 그 하위로 타고 내려간다 (더 일치하는게 있을지도 모르니. 일치하는 것이 탐색동안 나오지 않을 때 까지 탐색 후 없으면 그 옆에 추가하고 isEndOfNode 표시를 해준다.
노드 탐색
- root node의 자식 중 원하는 문자열이 첫번째 글자가 있는지 판단한다 -> 이후 한 층당 한 글자가 해당하는지 검사하고, 그 자식 노드로 계속 내려간다. 이때 하나라도 없으면 없는거...
- 문자열의 마지막 글자에 해당하는 노드가, isEndOfNode = false일 경우에도 존재하지 않는다. (얘가 끝인게 아니므로)
노드 삭제
- 노드 탐색 방법처럼 트리에서 삭제하고자 하는 문자열의 끝 노드로 이동한다. ( isEndOfNode = true인 상태)
- 노드를 삭제하는건 간단하다. isEndOfNode = false로 바꿔주면 됨!! (해당 글자를 끝으로 하는 문자열을 없다는 것이 되므로)
- 마지막 글자에 딸린 자식 노드가 있다면 거기서 끝난다 (이 단어를 삭제한다고 해도 밑에 애들이 쓰기때문에)
- 만약 자식 노드가 없다면, 더이상 필요없는 문자들이므로 거슬러 올라가며 삭제해준다. 이때 삭제 대상인 문자에 딸린 자식 노드가 (방금 삭제하고 올라온 노드를 제하고) 없어야만 삭제할 수 있다 (자식 있으면 거기서 탐색 끝!)
3. 트라이 구현
//#1. 노드 클래스
class Node {
HashMap<Character, Node> child; //key : 자식노드의 문자, value : 자식 노드의 Node 객체
boolean isEnd;
Node(){
this.child = new HashMap<>();
this.isEnd= false; // false로 설정
}
}
//#2. 노드들을 넣을 Trie 클래스
class Trie {
Node root;
Trie(){
this.root = new Node();
}
//특정 str 문자열 삽입
void insert(String str){
Node node = this.root;
for(i-> 0 ~ str.len){
char c = str.charAt(i);
//c가 자식노드 중 없는 경우 자식노드로 추가함
node.child.putIfAbsent(c, new Node());
//(없다면 방금 만든) c의 자식노드를 타고 넘어감
node = node.child.get(c);
}
//문자열 삽입이 끝났으므로 마지막 노드에 끝 표시 해줌
node.isEnd = true;
}
//특정 문자열 탐색
boolean search(String str) {
//자식노드들 중 찾고자 하는 문자들이 순서대로 있는지 확인
Node node = this.root;
for(i-> 0 ~ str.len){
char c = str.charAt(i);
//자식 노드에 c가 있는지 체크
if(node.childe.containsKey(c))
node = node.child.get(c);
else //문자 없는 경우
return;
}
//끝까지 다 찾은 것이므로 해당 노드가 끝인지 검사
return node.isEnd;
}
// 삭제 요청 시 먼저 작동하는 메서드 (삭제는 재귀로 타고 올라오며 진행되므로)
boolean delete(String str) {
boolean result = delete(this.root, str, 0); //현재 노드, 삭제대상, 몇번째 문자인지
return result;
}
boolean delete(Node node, String target, int targetIdx) {
char c = str.charAt(targetIdx);
//현재 노드에서 자식에 c가 없는 경우 (존재하지 않는 단어)
if(!node.child.containsKey(c)) return fasle;
//현재 노드에서 해당하는 자식 노드로 타고 넘어감
Node now = node.child.get(c);
tartgetIdx++;
//target의 끝인 경우 -> 얘부터 삭제해주며, 타고 올라가며 삭제 시작
if(targetIdx == target.length()){
if(!now.isEnd) return; //끝이 아닌 경우 -> 삭제 X
now.isEnd = false;
//해당 문자 밑에 다른 child 존재하지 않으면 아예 삭제
if(now.child.isEmpty())
now.child.remove(c);
}
//target의 끝에 도달하지 않은 경우 -> 재귀호출로 타고 내려감
else {
//삭제 실패한 경우
if(!this.delete(now, target, targetIdx))
return false;
// 삭제 성공하고, 얘의 자식노드도 없는 경우, 현재 노드도 삭제함
if(!now.isEnd && now.child.isEmpty())
node.child.remove(c) //node.childe.get(c) == now, 즉 now 노드 삭제
}
return true;
}
참고
반응형
'Algorithm' 카테고리의 다른 글
| [JAVA] 3459. 승자 예측하기 - SWEA (0) | 2024.05.05 |
|---|---|
| [JAVA] 4408. 자기 방으로 돌아가기 - SWEA (0) | 2024.05.04 |
| [다익스트라 / 플로이드-워셜] 알고리즘 정리 (0) | 2024.02.05 |
